Proof theory; Type theory; Functional programming (IMD0110)

The Curry–Howard isomorphism

Mailing list archive (members only)

Horários:4T12 [13h00–14h40]
Sala de aulas:A304
Sala do prof:A225
Horário de atendimento:mande email para marcar
Contato:thanos@imd.ufrn.br

Prerequisitos

  • maturidade matemática:
    • deve ser capaz de argumentar e se expressar matematicamente, em linguagem natural;
    • provar proposições direitamente e com técnicas comuns (por exemplo indução, absurdo, por casos, etc.);
    • saber os significados de implicação, equivalência, contrapositívo, leis básicos de lógica, De Morgan, etc.;
    • noções de teoria de conjuntos ingénua, operações e relações em conjuntos (por exemplo, união, intersecção, subconjunto, etc.);
  • pelo menos pouca experiência com lógica matemática
  • desejados:
    • Já ter cursado FMC2 ou a pegar em parallelo.
    • Experiência com programação funcional ajudaria mas NÃO será estritamente necessária.
    • Experiência com programação não-funcional (disfuncional) atrapalharia mas NÃO será estritamente proibida. ;)
  • óbvios: (óbvios para qualquer disciplina mesmo!)
    • {vontade, tempo} para {hackear, praticar, procurar, implementar, programar} nos assuntos da disciplina (não é uma disciplina "passiva"!)

Descrição

Nos vamos estudar teoria de típos, teoria de próvas, programação funcional, e o isomorfísmo Curry–Howard.

  • Lógica proposicional e de predicados
  • Lógica clássica e intuicionista
  • Teoria de tipos, tipos em linguagens de programação, inferência de tipos
  • Teoria de provas, natural deduction, sequent calculus
  • Lambda-calculus e lógica combinatória
  • Programação funcional: princípios, programação de ordem alta, Currying, tipos de dados abstratos, polimorfismo.
  • O isomorfísmo Curry–Howard
  • Tipos dependentes, programação e provas formais com tipos dependentes
  • Linguagens: Coq, Agda, Idris, Haskell, ...

O curso é introdutório mas com velocidade alta, e dependendo da participação dos alunos, poderia ser extendido com um "sequel", (parte II), no 2017.2 ou no 2018.1.

Bibliografia

(Conhece o libgen.io?)

(Por enquanto simultaneamente incompleta e redundante.)

Grading

Unit 1

Unit 2

  • Participation in class (“on the spot” solution of exercises / answers to questions)
  • Presentation of book chapter

Unit 3

  • Assignments from SF (implementations with deadlines; throughout the duration of the course)

Software Foundations: DEADLINES

Homework

22/02/2017

  1. Find a constructive proof of the theorem we proved classically:
    Existem irracionais x, y com xy racional.
  2. If you know what an algebraic number is, prove the following:
    Either π + e or πe is irrational. (Hint: π and e are transcedental.)

24/02/2017

  1. Show that all of the following formulas are intuitionistically valid:
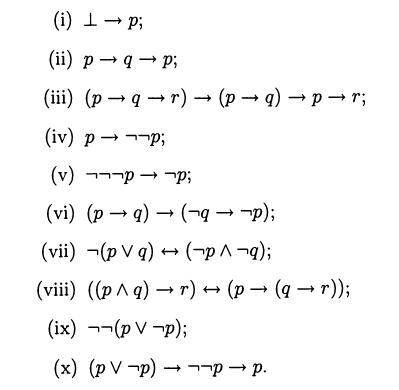
    intuitionistically valid formulas
    Obs.:
    ¬φ is an abbrev. for (φ → ⊥)
    (φ↔ψ) is an abbrev. for ((φ→ψ) ∧ (ψ→φ))

08/03/2017

  1. Using BNF, define a language of propositional logic L0 with parentheses, negation, disjunction, and conjunction. Then:
  2. Define the function height which returns the height of the syntactic tree of its input, considering atomic formulas p to be of height 0.
  3. Define the function length which returns the length of its input.
  4. The height of any formula is strictly less than its length.
  5. A proper prefix of a wff is not a wff.
  6. Define the function push which returns a formula logically equivalent to its input, on which negations have been “pushed” appear only in front of atomic formulas.

29/03/2017

  1. Using BNF, define a language of propositional logic L0 with parentheses, negation, implication, disjunction, and conjunction, without using «...».
  2. Show that both {↑} and {↓} are complete sets of connectives.
  3. Are {¬,+}, {+,∧,∨}, {¬,+,↔} complete? Prove your answer!
  4. Find proofs of:
    1. ⊢ A → A
    2. ⊢ (¬A → A) → A
    3. A → (B → C) ⊢ B → (A → C)
    4. ⊢ (¬B → ¬A) → (A → B)

12/04/2017

  1. Prove (without help!) that the Hilbert derivation system we use is sound:
    Γ ⊢ A ⇒ Γ ⊨ A
  2. Try to prove that the Hilbert derivation system we use is complete:
    Γ ⊨ A ⇒ Γ ⊢ A

26/04/2017

  1. Exercises 1.1–1.8 of Nederpelt & Geuvers
  2. Proposition (wrong!):
    Let M ∈ Λ, such that M → M1 and M → M2 Then M1 → N and M2 → N for some N ∈ Λ.
    Theorem (Church–Rosser):
    Let M ∈ Λ, such that M →…→ M1 and M →…→ M2. Then M1 →…→ N and M2 →…→ N for some N ∈ Λ.
    Theorem (weak Church–Rosser):
    Let M ∈ Λ, such that M → M1 and M → M2. Then M1 →…→ N and M2 →…→ N for some N ∈ Λ.
    (i) Show that the proposition above is false (find a counterexample).
    (ii) Pretend that the proposition is true, and use it to “prove” the C–R theorem.
    (iii) Prove the weak C–R (without using the C–R).
  3. Do all the previous exercises that you haven't done yet!

03/05/2017

  1. S(KS)K behaves like B does
  2. SKK behaves like I does
  3. Exercises 1.9–1.17 of Nederpelt & Geuvers
  4. Define a λ-term pair that can serve as a pair constructor, together with two projection functions (λ-terms) fst and snd, such that for any terms M, N:
    fst (pair M N) =β M
    snd (pair M N) =β N

04/05/2017

  1. Define a term comp such that comp f g = f∘g.
  2. Exercises 1.18–1.20 of Nederpelt & Geuvers
  3. Write a λ-term fib that computes the fibonacci sequence, and use it to calculate fib(3).
  4. Let Δ = (λx.xx). Show that Δ(f∘Δ) = f(Δ(f∘Δ))
  5. Let: 
        G       := λy.λf.f (y f)
    Y_1     := λf.Δ(f∘Δ)
    Y_{n+1} := Y_n G
    Prove:
    • (i) For all x, Y1 x = x (Y1 x)
    • (ii) G Y1 = Y1
    • (iii) For all x, Yn x = x (Yn x) [for all n≥1]
    • (iv) G Yn = Yn [for all n≥1]
    Hint: (i) & (ii) serve as bases for (iii) & (iv) respectively.
    ♥-level interpretations:
    • (iii): «all the Yn are fixpoint combinators»
    • (iv): «all the Yn are fixpoints of G»
  6. Solve the problems of ornithology_101.pdf.

Lessons log

15/02/2017: Apresentação do curso e dos participantes

22/02/2017: Intuitionistic logic: The BHK interpretation

24/02/2017: The untyped λ-calculus: ideas and notation

08/03/2017: Formal languages; recursion – induction

29/03/2017: Mathematical logic: propositional calculus

  • Syntax & semantics
  • Proof theory & model theory
  • Complete sets of connectives
  • Hilbert-style proofs
  • The system H0:
    • MP. (Modus Ponens): Infer β from α → β and α
    • H1. α → (β → α)
    • H2. [α → (β → γ)] → [(α → β) → (α → γ)]
    • H3. (¬β → ¬α) → [(¬β → α) → β]

12/04/2017: Mathematical lógic: propositional calculus

  • Hilbert-style proofs
  • ⊢ A → A
  • Deduction theorem
  • Soundness and completeness

26/04/2017: The untyped λ-calculus

  • §§1.1–1.9 of Nederpelt & Geuvers
  • Syntax and conventions
  • Metalanguage; metavariables; metanotation
  • Renaming
  • Substitution
  • α-equivalence
  • β-redex; one-step (→)/many-step (→*) β-reduction; β-nf (normal form)
  • weakly normalizing; strongly normalizing
  • β-equivalence
  • η-equivalence
  • Church-Rosser theorem (CR)
  • A corollary: M =β N ⇒ existe L com M →* L *← N

03/05/2017: Combinators; Church numerals; Arithmetic and boolean logic within λ

  • Barendregt convention
  • β-normal forms (exercises)
  • Combinators in λ
  • The Curry–Howard correspondence: Hilbert proofs and combinators
  • The combinators I, K, B, Q, S
  • The expressive power of K, S
  • The combinators S(KI) and BI behave like I does
  • Natural numbers in λ
  • Arithmetic in λ: succ, plus, times, exp, pred, …
  • Boolean logic in λ: true, false, logical operators (not, and, or, xor, implies), iszero, if-then-else, …

10/05/2017: λ-calculus

  • Solving equations in which the unknown is a function
  • The least solution
  • Fixpoints
  • Defining functions by recursion
  • The Y-combinator
  • Calculating recursively defined functions (e.g., factorial)
  • Bizarre properties of λ: self-applications; divergent terms; all λ-terms have fixpoints!

24/05/2017: Proof theory

  • Natural Deduction

31/05/2017: Proof theory

  • Natural Deduction
  • Dynamic of proofs
  • Proof normalization as computation

09/06/2017: Proof theory

  • Sequent calculus (LK & LJ)
  • Linear logic
  • Cut elimination

14/06/2017: Written exam

21/06/2017: Presentation 1

  • Simply typed lambda calculus, by Bianca & Elias

23/06/2017: Presentation 2

  • System F, by Gabriel & Marciel

28/06/2017: Presentations 3 & 4

  • Types dependent on types, by Luis & Ronaldo
  • Types dependent on terms, by JP & Luísa

Last update: Fri Jun 30 04:55:29 -03 2017